Think Space - 思考空間: febrero 2011

ΑΓΕΩΜΕΤΡΗΤΟΣ ΜΗ ΕΙΣΙΤΩ

Intuition behind the Laplacian and the Adjacency matrix of a Graph

Consider a graph G(V,E). There are several different matrix representations of this graph. As this is one of the first posts in a series of posts I plan to do on spectral graph theory, I think it makes sense to elaborate a little bit on the different intuition behind the adjacency matrix representation and the Laplacian (for some people the correct spelling is Laplacean but anyway, I will stick to Laplacian).

Let $A_G$ be the adjacency matrix of G(V,E) and $L_G$ its Laplacian matrix.

There are two types of Laplacians, the combinatorial and the normalized one.

In this post, I will refer to the combinatorial Laplacian.

So let’s do a small MATLAB experiment for the Laplacian, since most people,

1) Generate a simple random graph.
    A = rand(30)<=.5;
    A = triu(A,1) ;
    A= A + A’;

2) Create the Laplacian of the graph
    L = diag(sum(A)) – A;

3) Now choose a subset of vertices $S \subseteq V(G)$ , and write down the corresponding indicator vector $x$ , where $x_i=1$ if node i belongs to set S, otherwise $x_i = 0$ .

Consider now the result of the matrix vector multiplication $y = Lx$ .

Let’s choose 5 random positions:
     x=zeros(30,1);
     tmp = randperm(30);
     pos = tmp(1:5);
     x(pos)=1;

and let’s perform the matrix vector multiplication y=L*x. Now,

if you run the following command: find(y>0) you will just get exactly the entries of the vector pos.

Now let’s look the other entries of the y. Some of them are 0 and some of them are -1. In the random experiment that I did, y(8) was zero.

Examining node 8, i.e., to which other nodes it’s connected, gives that it is not connected to any of the nodes in set S! Whereas all entries i where y(i)<0 are connected with one of the nodes in S (and as I said above using the bold word exactly, i is not in S).

The observations of this simple experiment, can be verified rigorously.

Consider $y_i=(Lx)_i= \sum_{j \in S} L_{ij}$ .

By the definition of the Laplacian we know that $L_{ii}= d_i$ , $L_{ij} = -1$ if $(i,j) \in E(G), i \neq j$ otherwise $L_{ij}=0$ .

Thus $y_i > 0$ is $i \in S$ and there are less than $d_i$ -1′s in the sum, since if we had exactly $d_i$ -1′s in the sum, $y_i$ would be zero.

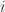But what does it mean to have less than $d_i$ -1′s in the sum? It simply means that there are some edges that node $i$ participates in, that “leave” the set S.

In other words $y_i>0$ is $i \in S$ and there exist at least one edge $(i,j) \in E(G)$ , but j not is S.

Now consider the case where $y_i =0$ .

This can happen in two cases. Either when all terms in the some are non-zeros or all zeros.

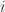Thus $y_i=0$ iff node $i$ belongs in S, or in V-S and no edges leave 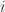$i$ to “go” to the other set of nodes.

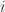Finally with the same piece of reasoning, $y_i<0$ means that node $i$ is not in set S, but there are edges $(i,j) \in E(G)$ such that $j \in S$ .

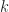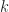To sum up, since the $k$ -th power $A^k$ gives us paths of length exactly $k$ (assume no self-edges, otherwise we get paths of length $\leq k$ ) we see what is the main difference between the Laplacian and the Adjacency matrix:

Adjacency matrix is “telling” us information on the numbers of paths,
the Laplacian is “telling” us information on the connectivity of the graph.

viernes, 25 de febrero de 2011

Intuition behind the Laplacian and the Adjacency matrix of a Graph

Intuition behind the Laplacian and the Adjacency matrix of a Graph