Think Space - 思考空間: 2011

jueves, 8 de septiembre de 2011

念頭不可隨便亂動

人，最容易控制的就是自己的心念；最不好控制的卻是自己的身體。我們可以決定要想先什麼，但我們卻不能為我們身體決定些什麼！

但現代的人，或許都犯了一種迷思，就是控制身體比控制心念還要容易，於是一直追求能控制身體的方法（美容、健身）。但到最後，人會發現，身體是會生、老、病、死的。不論在吃些什麼要，身體也由不得你來控制。

相對的，心念，卻是我們自己的，他不會隨著時間而有生、老、病、死的轉變。反倒是，隨著時間，我們會愈來愈習慣往某一些方向去想，這應該就是現代人所謂的「慣性思考」。

我今天，想了許久，我發現，我只要自己在家工作，我的念頭都是充滿了很無趣的想法，比如說埋怨、責怪他人、要求環境來配合我等等…。但是我現在對「念頭不可亂動」這句話，有更加一層的體悟了。人只要一動念，念頭的能量馬上就到來自己的身上。動的是負面的，負面能量就來；動的是正面的，正面的能量就來。若動的是符合整個宇宙意識的，則宇宙的能量就是源源不絕的過來。

所以，當我了解這個真理後，我對念頭不可亂動這句話，又多加了些重要性。我就是太隨便動念，所以我的靈魂充滿了各種不同的能量，有好、壞、正、負，最後因為冰炭不同爐，我連自己該動什麼念都不知道了。所以我顯得散慢，思緒繁亂了。

無怪乎，在禮記大學篇中所言：「知止而後有定！」人一定不能隨便動念，一隨變動念，則心神不定，在不定的狀態下，眼睛就看不清楚，連聽都聽不清楚了。

古代的聖人真是明智阿！

總的來說，人要動什麼念，都是由自己決定的。天堂地獄，自心間阿！還是要多以正面的思考、想法去動才會讓自己這短暫的人生充滿一些光輝、活得更快樂、也更能為這天地間帶來許多光明！

人不知而不慍，不亦君子乎

論語的頭一篇的一開頭，就提到了：「學而時習之不亦悅乎，有朋自遠方來不亦樂乎，人不知而不慍，不亦君子乎。」

因為這是聖人的話，當然也只有聖人才能完全的理解。對我這種汙穢的眾生而言，只能再次用我淺薄的意識和低下的修為來論談了。

其實我對「人不知而不慍不亦君子乎」似乎是情有獨鐘。
為什麼這樣說呢？很多時侯，我都會想：「如果他人怎樣，我就會怎樣…如果他人對我所期待的有所做為的話，而我就會更好怎樣之類的！」但是，一直期待別人來為我負責，幫我做事，這不是一種自私的心態嗎？好像就是讓別人累，而我來享受。這樣看來就是一種自私的態度。這樣又怎麼能算的上是一個上帝的兒子（君子）呢？

所以，就算我們心中很期待某些人做某些事，我們也不必因為別人不知道我們心中的期待而生氣。有期待，不是不好的。就好像爸媽會期待子女們成長成熟，這又沒有什麼不對。中國有句成語說：「望子成龍，望女成鳳。」這是一個正常的心理狀態。但是身為兒子的我們，有去了解過父母親的期待是什麼嗎？而一個真正的父母親真的會希望兒子能了解他內心的期待嗎？還是他們只是期待著兒女們能夠成熟和成長嗎？

以我這種低智商的人來看，真正的父母，的確會希望兒女了解他的心意，但他不會因為兒女不了解而生氣、埋怨。現代的人，對是希望被別人理解，但是總藏著一股怒氣在心。而古代的人，雖然也希望被人了解，但是他們的心卻沒有怒氣。

古代的人，希望被誰了解呢？
現代的人，又希望被人了解什麼呢？
古代的聖人們，又希望被誰了解呢？

有關這三個問題，我的認為是：
古代的人，希望被有德性的人理解。很夠時侯，志士仁人們的作為，凡夫俗子是不可理解的，所以孟子才說：「君子之所為，眾人故所不識也！」但他們知道，唯有真正的志士和仁人，才會理解他們所做的是什麼，故死而無憾。

現代的人，又希望被什麼人了解呢？可能是希望被全世界的人了解吧。但這是一種妄想，只會讓自己痛苦而矣。他們希望被了解些什麼呢？若不是一個志士仁人，恐怕被人了解的就是自己的個性、想法、作為而矣，這沒有什麼意義，歷史也不會因為你而改變。反之，一個志士仁人，不管是古代還是現代，他們只希望上帝了解他們的一切做為是無私的、無怨的、無痴的。這又是多麼的光明阿！

古代的聖人希望被誰了解呢？哈哈…我想，他們想被人了解的應該就是天意，而不是自己的想法；所以他們希望被全世界了解，因為他們本身就是真理了。但這種境界，非由我這樣低賤的靈性可以去體會的，只能用猜測而矣。

總而言之，我現在該學的就是要接受一個事實：當人不了解我時，我沒有必要生氣！這是成為一個君子的最初的條件。

今天就發表到這裡，有任何文不達義之處，還請各位見諒！

miércoles, 7 de septiembre de 2011

君子可欺之以方，不可罔之以非其道

《孟子·萬章上》
孟子曰：“昔者有饋生魚于鄭子產，子產使校人畜之池。
校人烹之，反命曰：‘始舍之圉圉焉，少則洋洋焉，攸然而逝。
’子產曰‘得其所哉！得其所哉！’校人出，
曰：‘孰謂子產智？予既烹而食之，曰：得其所哉？得其所哉。’
故君子可欺以其方，難罔以非其道。”

看了這段話，起初並不是很了解，是因為無意中記起了「把凡事做最好的翻譯」這句話，而有更深一層的體會。我常常懷疑，很多時侯，智者明明知道他是被騙，但又得想別人沒有騙我…這樣不是很矛盾嗎？這樣會不會得雙重人格？一個人格是凡人對待心態；別一個則是智者的心態…？若我明知道他欺騙我，而我又裝做它沒有欺騙我，那我準得精神分裂。

但既然是聖人說的話，聖人是正確的，為什麼孟子聖人要這樣說呢？

我想，這應該只聖孟子聖人才能明確知道他為什麼這樣說，我這個輪迴多次的凡夫俗子只能用我淺薄的知識來解讀了…

聖人，既然是成聖了，他的心就是光明，他對大家都是平等心，都是給大家光明。然而當他受騙時，他並不會讓「受騙」這個陰影靠近他的心，他只有把這「陰影」給轉化成好的一面。也就是，他明知道魚是被殺了吃了，而人又騙他魚自己遊走了，他還是告訴自己：「太好了，魚終於得到了自由」。他這樣說的原因有二：一）讓自己不要去猜別人的心，不度人腹。２）用這個正面的想法，以心連心的方式告訴大家，魚最好讓它活，讓它也得到自由，這樣是最快了的。

我認為，我應該要多多學習這種轉念的方式，讓環境變得更美滿才對，而不是一味的埋怨和恨惡。

再記一次：「把凡事做最好的翻譯！」，告訴我自己嘍。

所以君子可欺子以方的另類翻譯：上帝之子，是可以用真理來欺騙自己。

下面那一句話：「不可罔之以非其道」，就可能是一種告誡。也就是說，就算用真理來欺騙自己，但不可以用真理來說服自己做不是該做的事。舉例來說，明明我知道懈怠不好，但因那一句真理：「休息是為了走更遠的路」，結果我就一睡到明年…這樣的欺騙是不好的，會讓自己更「罔」，也就是更無力而矣。

懦家的教義，真的是兩面都考慮到了。太偉大了！

jueves, 1 de septiembre de 2011

A cazón quitado - 被…用教訓的口氣對待

La frase coloquial(口語上) a calzón quitado se entiende como conversar con precisión y franqueza（直率). El Diccionario de la Lengua Española incluye esta expresión y la define como hablar claro. Esta locución habría surgido de la antigua, y felizmente desterrada(廢除的), costumbre de castigar a los niños en los colegios con una palmeta(責打學生用的戒尺), un instrumento de madera, aplanado en uno de sus extremos, con el cual se golpeaba a pequeños y adolescentes en las manos o en el culo. Cuando se trataba de una falta grave, era usual que se cambiase la palmeta por un chicote(鞭子) y si la trastada(胡鬧) era muy grave, el alumno debía concurrir a(去參加、去報到，ir a...) disculparse a la oficina del inspector escolar de turno donde, luego de las explicaciones, se bajaba los pantalones y calzoncillos, para que los palmetazos o chicotazos que se le propinaran(給一頓訓斥、毆打) fueran... a calzón quitado o a poto pelado, como se dice coloquialmente. Luego del castigo, el sancionado comentaba a sus condiscípulos(同學) que había mantenido con la autoridad una dolorosa conversación a calzón quitado. Todos entendían que había recibido una buena zurra(鞭打) en el traste(屁股).

這一句話，是在智利當地耳熟能詳的。看了他的出處，才知道它的意思並不是內褲被脫掉，而是指當沒有外在的保護而生生的被痛斥，才會學的乖的意思。我們可以說：Me enseñaron a calzón quitado，也就是：「用硬派的方式教導我；用最直接的語氣教導我。」

好，這是今天學到的一句話。若有不足，請海內外各高明能夠不吝指正，讓我們一起進步吧！

viernes, 25 de febrero de 2011

Intuition behind the Laplacian and the Adjacency matrix of a Graph

ΑΓΕΩΜΕΤΡΗΤΟΣ ΜΗ ΕΙΣΙΤΩ

Intuition behind the Laplacian and the Adjacency matrix of a Graph

Consider a graph G(V,E). There are several different matrix representations of this graph. As this is one of the first posts in a series of posts I plan to do on spectral graph theory, I think it makes sense to elaborate a little bit on the different intuition behind the adjacency matrix representation and the Laplacian (for some people the correct spelling is Laplacean but anyway, I will stick to Laplacian).

Let $A_G$ be the adjacency matrix of G(V,E) and $L_G$ its Laplacian matrix.

There are two types of Laplacians, the combinatorial and the normalized one.

In this post, I will refer to the combinatorial Laplacian.

So let’s do a small MATLAB experiment for the Laplacian, since most people,

1) Generate a simple random graph.
    A = rand(30)<=.5;
    A = triu(A,1) ;
    A= A + A’;

2) Create the Laplacian of the graph
    L = diag(sum(A)) – A;

3) Now choose a subset of vertices $S \subseteq V(G)$ , and write down the corresponding indicator vector $x$ , where $x_i=1$ if node i belongs to set S, otherwise $x_i = 0$ .

Consider now the result of the matrix vector multiplication $y = Lx$ .

Let’s choose 5 random positions:
     x=zeros(30,1);
     tmp = randperm(30);
     pos = tmp(1:5);
     x(pos)=1;

and let’s perform the matrix vector multiplication y=L*x. Now,

if you run the following command: find(y>0) you will just get exactly the entries of the vector pos.

Now let’s look the other entries of the y. Some of them are 0 and some of them are -1. In the random experiment that I did, y(8) was zero.

Examining node 8, i.e., to which other nodes it’s connected, gives that it is not connected to any of the nodes in set S! Whereas all entries i where y(i)<0 are connected with one of the nodes in S (and as I said above using the bold word exactly, i is not in S).

The observations of this simple experiment, can be verified rigorously.

Consider $y_i=(Lx)_i= \sum_{j \in S} L_{ij}$ .

By the definition of the Laplacian we know that $L_{ii}= d_i$ , $L_{ij} = -1$ if $(i,j) \in E(G), i \neq j$ otherwise $L_{ij}=0$ .

Thus $y_i > 0$ is $i \in S$ and there are less than $d_i$ -1′s in the sum, since if we had exactly $d_i$ -1′s in the sum, $y_i$ would be zero.

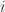But what does it mean to have less than $d_i$ -1′s in the sum? It simply means that there are some edges that node $i$ participates in, that “leave” the set S.

In other words $y_i>0$ is $i \in S$ and there exist at least one edge $(i,j) \in E(G)$ , but j not is S.

Now consider the case where $y_i =0$ .

This can happen in two cases. Either when all terms in the some are non-zeros or all zeros.

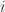Thus $y_i=0$ iff node $i$ belongs in S, or in V-S and no edges leave 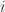$i$ to “go” to the other set of nodes.

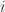Finally with the same piece of reasoning, $y_i<0$ means that node $i$ is not in set S, but there are edges $(i,j) \in E(G)$ such that $j \in S$ .

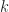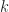To sum up, since the $k$ -th power $A^k$ gives us paths of length exactly $k$ (assume no self-edges, otherwise we get paths of length $\leq k$ ) we see what is the main difference between the Laplacian and the Adjacency matrix:

Adjacency matrix is “telling” us information on the numbers of paths,
the Laplacian is “telling” us information on the connectivity of the graph.